In this blog post, I will discuss the class of attacks known as side-channel attacks (SCA), how masking is an effective countermeasure against SCA, why masking Dilithium is difficult and how we designed our masking-friendly scheme Raccoon!
In 2022, NIST unveiled the first schemes selected to be NIST PQC standards: Kyber for key encapsulation, and Dilithium, Falcon, and SPHINCS+ for digital signatures. The security of these schemes has been extensively studied, and the community are confident in their mathematical foundations (lattices and hash functions). However, when deploying them one should pay special attention to side-channel attacks.
Side-channel attacks (SCA)
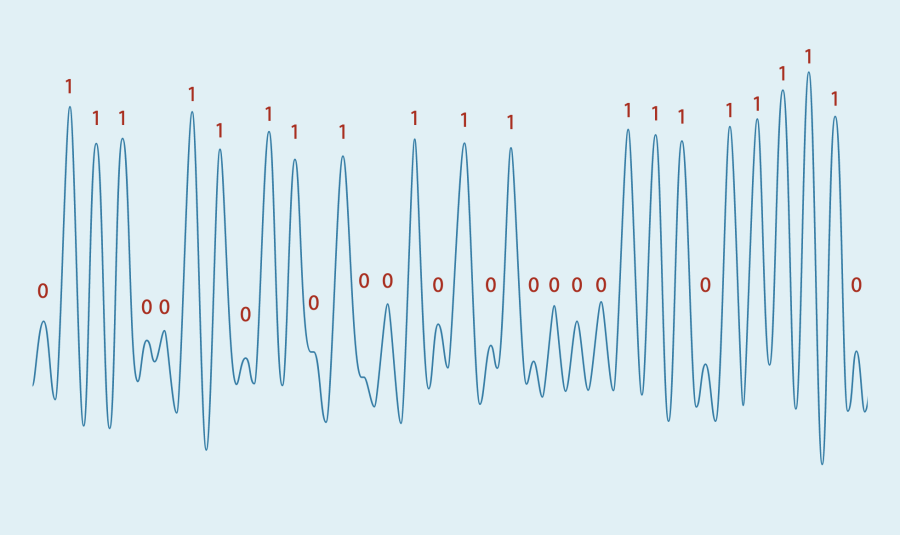
When a physical device executes an algorithm, it may physically leak information about the type of operation, or the data being processed. For example, a computationally expensive operation may drain the battery of your smartphone or heat it up. This leakage may manifest via other forms, such as the running time, electromagnetic emissions, or acoustic emission of the device. Sometimes, even the distant flickering of a LED can be exploited (Ars Technica). The umbrella term side-channel attacks (SCA) encompasses all attacks that leverage such leakage to compromise sensitive data. This toy example from a research paper (ACM) displays the electric potential of a laptop using an RSA private key to decrypt a message. We can see a clear correlation between the bits of the private key (in red) and the signal being measured (in blue).
Post-quantum schemes are no less vulnerable to SCA than their classical counterparts. For example, several SCA have been demonstrated against Dilithium (PQCrypto, TCHES). In contexts where SCA can be mounted, it is vital to adopt countermeasures against SCA.
Defeating SCA with masking
There exist many ways to mitigate SCA. I will focus on masking, since it is the most studied countermeasure, as well as one of the most generic, most effective and most common. Masking consists of splitting each sensitive variable into d random shares, such that adding all shares recovers the variable. For example, consider x = 9 in ℤ16, where ℤ16 is the ring of integers modulo 16. A valid masking of x with 3 shares would be (12, 5, 8), since (12 + 5 + 8) mod 16 = 25 mod 16 = 9.
The idea behind masking is that sensitive data is distributed across several shares, making it harder for an attacker to simultaneously learn the values of all shares. Experiments and analyses show that when masking with d shares, the cost of an attack increases exponentially in d. This gives us a reason to set d as high as possible.
The hard part, however, is that we need to be able to perform useful operations on masked data. Some operations are easy to perform. Addition modulo q is one of them: (12, 5, 8) is a valid sharing of 9, (7, 2, 10) is a valid sharing of 3, and one can see that ((12 + 7) mod 16, (5 + 2) mod 16, (8 + 10) mod 16) = (3, 7, 2) is a valid sharing of 9 + 3 = 12. Note that this only requires d additions in the ring ℤ16, so masked addition is an efficient operations. More generally, linear operations (including multiplying a masked vector by a matrix) are easy to mask efficiently. However, not all operations are easy to mask.
Why masking Dilithium is difficult
Now, let us have a look at the Dilithium signature scheme. We use bold lowercase notation for vectors (s, w, r, z), and bold uppercase for matrices (A). In Dilithium, the private key is a short vector s and the public key is the pair (A, t = A ⋅ s), where A is a large, random matrix. The signing procedure, very simplified, goes as follows:
- [Sample] Sample a short secret vector r
- [Linear] Compute a commitment w = A ⋅ r
- [Decompose] Decompose w in its high-order and low-order bits: w = w0 + 2k ⋅ w1.
- Compute a challenge c = H(msg, w1)
- [Linear] Compute a response z = c ⋅ s + r
- [Reject] If z is not in a given interval S, go to step 1.
- Output the signature sig = (c, z)
Now, suppose we want to mask Dilithium. What should we do?
- It has been argued in research papers that Steps 4 and 7 never need to be masked, so we won’t mask them.
- Steps 2 and 5 manipulate sensitive data and therefore need to be masked. Since they are linear operations, they can be masked efficiently; we mark them with a nice [Linear] tag.
- The remaining steps are Step 1 [Sample], Step 3 [Decompose] and Step 6 [Reject]. They manipulate sensitive data and need to be masked; however this will be a difficult task.
In order to understand why Steps 1, 3 and 6 are problematic, we need to introduce Boolean masking. The definition of masking that I introduced earlier is called arithmetic masking, because we work in the arithmetic ring (ℤ16, +). However, nothing prevents us from using the binary representation of numbers instead, and to do all operations in the Boolean ring ((ℤ2)4 , ⊕), where ⊕ is the binary xor operator. For example, the binary representation 9 is 1001, and a valid masking of 1001 in (ℤ2)4 is (0101, 0010, 1110) since 0101 ⊕ 0010 ⊕ 1110 = 1001. This type of masking is called Boolean masking. Switching between arithmetic and Boolean masking is called mask conversions, and is an expensive operation, so we would like to avoid it.
Back to Dilithium, let us consider the step [Decompose]. Decomposing a number in its high-order bits and low-order bits is a simple computation: for example, 9 = 1 + 22 ⋅ 2. Bit-decomposition commutes with Boolean masking: the bit-decomposition of a Boolean masking is also a Boolean masking of the bit-decomposition. For example, if we decompose (0101, 0010, 1110) in its high-order bits (01, 00, 11) and low-order bits (01, 10, 10), we can see that 01 ⊕ 00 ⊕ 11 = 10 and 01 ⊕ 10 ⊕ 10 = 01. The bitstrings 10 and 01 are indeed the binary representations of the decomposition of 9 (2 and 1).
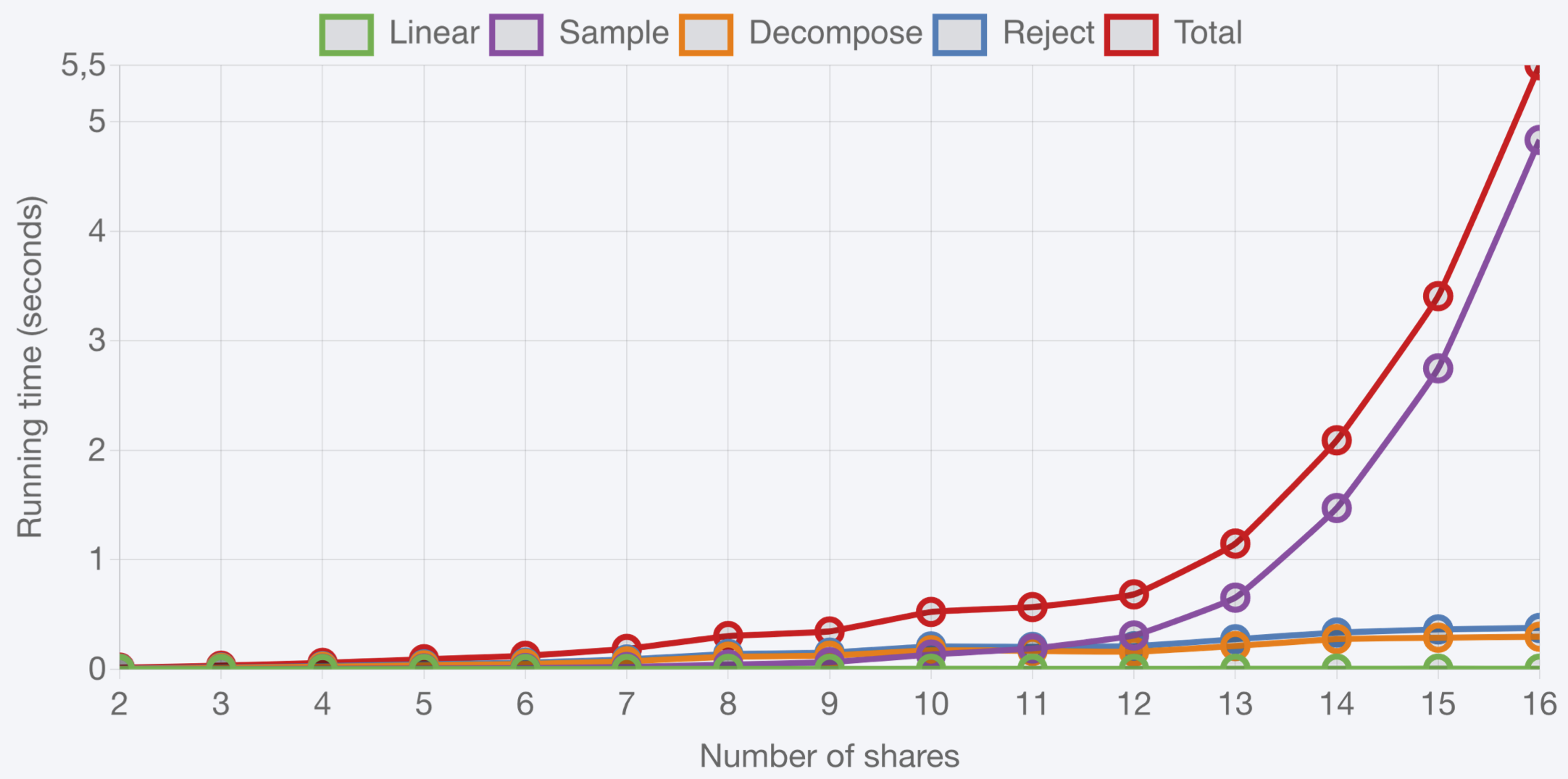
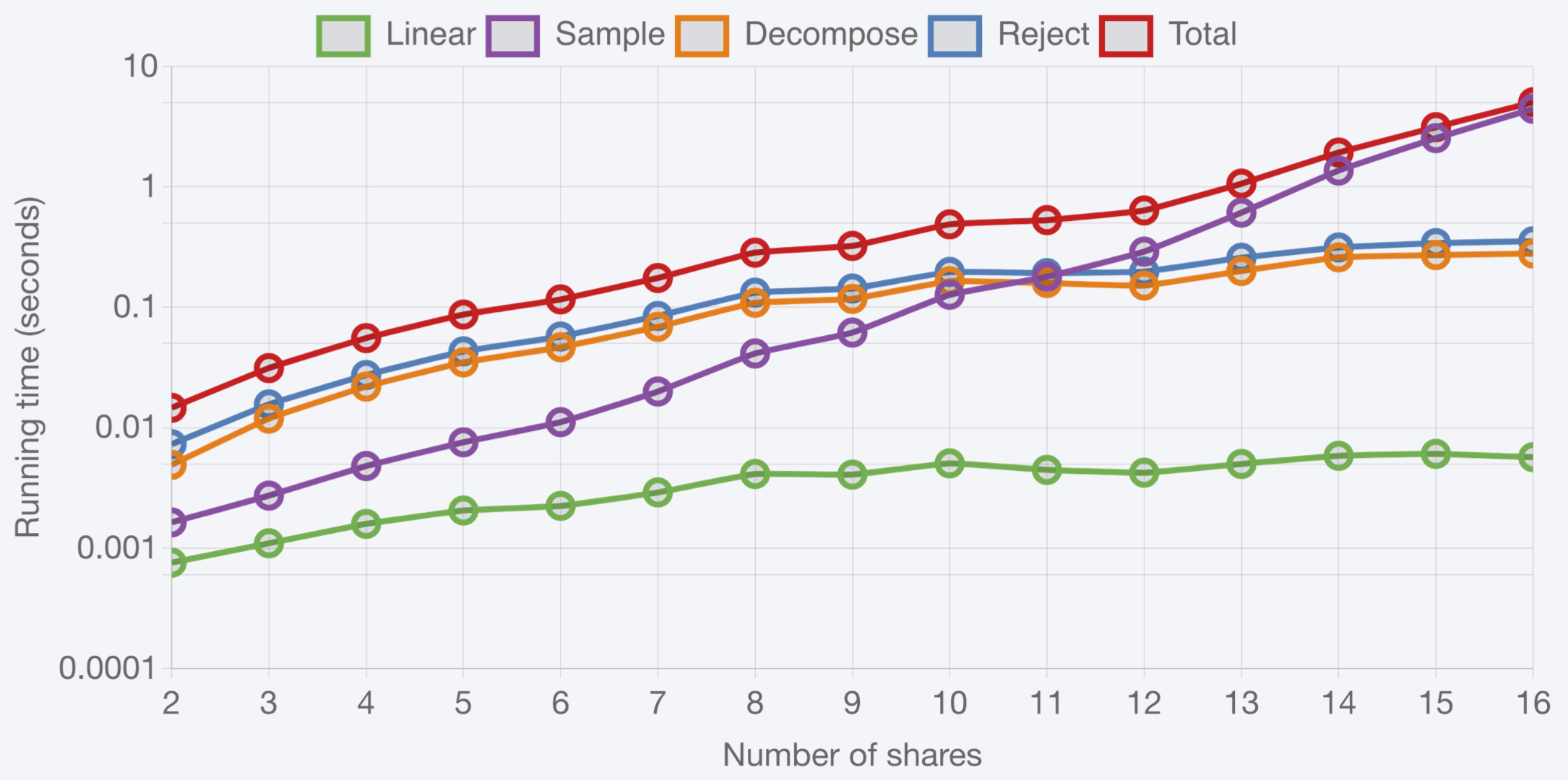
Unfortunately, there does not seem to be an easy way to compute [Decompose] in arithmetic masked form efficiently. As of today, the best known approach is to switch from arithmetic to Boolean masking using a mask conversion, then perform [Decompose] in this representation. The Steps 1 [Sample] and 6 [Reject] suffer from similar issues. Simply put, there is no known way to mask Dilithium without using expensive mask conversions. The blow-up in running time when masking Dilithium makes it unrealistic to reach high masking orders, as illustrated below using an open source implementation (GitHub) from a recent paper by researchers at IDEMIA and Université du Luxembourg (TCHES). These numbers were obtained on a desktop with Intel Core i7 7700T @ 2.9 GHz. We can see in these graphs that [Decompose], [Reject] and especially [Sample] make up most of the cost of masked Dilithium.
Raccoon: a masking-friendly PQC signature
In Summer 2021, the side-channel limitations of Dilithium were already well-documented. This motivated my colleague Rafael and myself to try and come up with an alternative design. This seemed difficult as three steps ( [Sample], [Decompose], [Reject] ) were difficult to mask, and changing or removing any of these three steps in isolation seemed to render the scheme insecure.
Our first breakthrough came in Fall 2021, when we realized that we needed to consider these three steps together, with [Reject] being the key step tying them all together. [Reject] was here to enforce a security notion called the ”zero-knowledge” property using a so-called “rejection sampling” security argument. We realized that by carefully adjusting parameters, one could remove [Reject] and still preserve the zero-knowledge property, by making a different analysis based on the Rényi divergence, a proof technique that had done wonders in the past for lattice-based cryptography, and which I had used back in 2017 to improve the efficiency of the Falcon signature scheme (ASIACRYPT).
Removing [Reject] created a domino effect. First, our Rényi divergence proof strategy made it completely unnecessary to mask [Decompose]. While [Sample] still needed to be masked, our proof technique was very flexible in this regard, which allowed us to come up with new algorithmic techniques that allowed us to perform [Sample] very efficiently.
While we got the skeleton of a scheme, we needed to turn this into a polished scheme. Fortunately for us, we had many colleagues at PQShield who excelled at what we needed: Markku is is highly skilled in highly efficient and secure embedded implementations, Shu and Mary are experts in security proofs, Thomas Espitau is savvy in lattice cryptanalysis and parameter selection, and Fabrice (now at XWIKI) has a good transverse understanding of all these aspects. Outside PQShield, we enlisted the help of Mélissa Rossi (ANSSI), an expert in security proofs for masking schemes. By combining the skills and ideas of this team of great people, we submitted to the NIST PQC call for additional signatures a scheme, Raccoon, that can be masked at high orders with minimal overhead, and orders of magnitude faster than Dilithium, as illustrated in this final figure: even with 8 shares, our unoptimized implementation of masked Raccoon is already 50 times faster than the optimized implementation of masked Dilithium.
Why this name? One of the most distinctive features of raccoons ? is the “mask” around their eyes. Thus we called our scheme Raccoon as a nod to its masking-friendly nature. If you want to read more about Raccoon, have a look at our website, NIST PQC specification and implementations!