Signal recently announced the Sparse Post Quantum Ratchet (SPQR). This update brings stronger post-quantum security to millions of Signal users. Combining SPQR with the existing Double Ratchet algorithm offers strong post-quantum security while maintaining all of Signal’s existing security properties and remaining very bandwidth-efficient. In this post, we explain how we helped Signal develop SPQR and the role it plays in the new Triple Ratchet protocol.
Modern secure messaging applications
Messaging applications like Signal, WhatsApp, Google RCS, and Facebook Messenger have become an invaluable tool in the everyday life of billions of people. At a technical level, the application provider typically needs to queue messages on a server. This is important because users expect to be able to send and receive messages even if their conversation partner is offline, relying on the application provider to deliver them as soon as possible. The exchanged messages, however, may contain intimate details that users might not feel too happy about being broadcast to the world. Thus, the applications are expected to satisfy strong security guarantees, in particular end-to-end encryption. This means messages remain hidden even from the application provider, and is achieved by encrypting them using keys only known to the communicating parties (the “ends”).
Chats on messaging applications tend to be long-lived, with a typical conversation often going on for years. As a consequence, Signal’s famous Double Ratchet protocol, which has become a de facto standard for secure messaging — used by not only Signal but also by WhatsApp, Google RCS, and Facebook Messenger — aims to retain security even in the case that user’s phones might temporarily get compromised. In this case, all cryptographic secrets leak to an adversarial party. While this inevitably leads to a compromise of current messages, we still want to provide security for messages sent before the compromise. Additionally, once the compromise event is over (for example, a software update fixes a bug), we would like the conversation to regain security after a short recovery period.
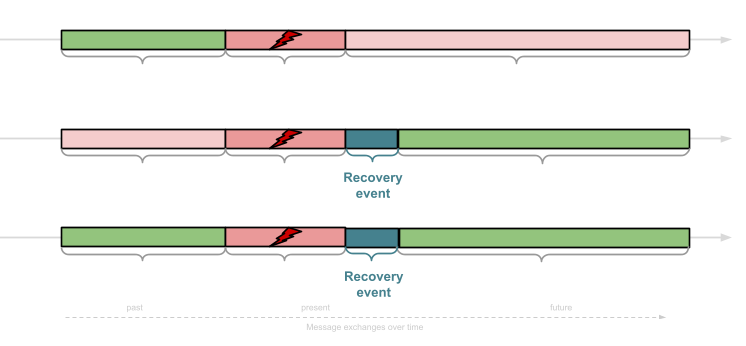
More formally, the secrecy of messages in the past is covered by what is denoted by forward secrecy (FS). This requires that all messages sent before the compromise (and were deleted from the phone’s chat history) remain secret. The latter is referred to as post-compromise security (PCS). This property states that if the users keep exchanging messages, the conversation becomes secure again after a short while, i.e., the adversary will no longer be able to decrypt the exchanged messages. To minimize the impact of a compromise, the Double Ratchet protocol provides both FS and PCS.
The Signal Protocol: a closer look
To meet these strong security requirements, the Signal Protocol constantly rotates the used cryptographic material and, in particular, encrypts every message under a distinct key. Conceptually, the protocol consists of two components: the handshake protocol and the public-key/symmetric ratcheting protocols (i.e., Signal’s Double Ratchet protocol).
- The initial handshake is used once at the very beginning of the conversation to establish a shared secret between both parties and provide authenticity guarantees. This was formerly handled by Signal’s X3DH protocol, recently updated to the harvest-now-decrypt-later secure PQXDH protocol.
The following two ratchets combine to form the Double Ratchet protocol:
- The symmetric ratchet is the main tool used to achieve forward secrecy. Whenever a message is sent or received, it ‘ratchets forward’ the key used to encrypt or decrypt the corresponding ciphertext to obtain an updated key, which in turn will be used for the next message. Now, if an adversary compromises the updated state, they will not be able to undo the ratcheting operation, and, importantly, neither decrypt prior protocol messages. As its name suggests, the symmetric ratchet relies exclusively on symmetric cryptographic primitives.
- The public-key ratchet is the tool allowing us to achieve post-compromise security (PCS). At a high level, it is used to regularly infuse fresh secrets into the chain of keys produced by the symmetric ratchet. Note that for PCS we need these secrets to remain hidden even from an adversary that had full access to a user’s previous internal state. As a consequence, the public-key ratchet relies on public-key encryption and, as we will see below, essentially consists of users sampling and sending public keys, as well as ciphertexts generated with respect to them.
The looming quantum threat
In its original form, the Signal Protocol did not provide post-quantum security: While the text messages are encrypted using symmetric encryption which is widely believed to remain secure even against a quantum computer, recall that these keys are exchanged using public-key cryptography. Specifically, both the initial handshake and the public-key ratchet are implemented using elliptic-curve cryptography. This makes the protocol particularly efficient, but could, unfortunately, be broken using a cryptographically relevant quantum computer.
In particular, the protocol was susceptible to so-called harvest-now-decrypt-later (HNDL) attacks. In such an attack, a large-scale adversary, while not being able to currently break the used encryption, simply records all encrypted messages. Once a cryptographically relevant quantum computer becomes available, this adversary would then be able to recover the encryption keys from the sent protocol messages, and in turn decrypt all sent text messages.
In 2023, Signal took a great first step towards amending this threat by replacing the elliptic-curve based X3DH handshake by a protocol denoted PQXDH. This protocol, as the name suggests, is no longer solely based on Diffie-Hellman (i.e., elliptic-curve based) cryptography, but also includes the exchange of a shared secret using the recently standardized post-quantum secure key-encapsulation mechanism ML-KEM by the United States National Institute for Standards and Technology (NIST). While this modification was a great first step towards post-quantum secure messaging, it only prevents HNDL attacks against passive adversaries: Assume that at some point after the initial handshake one of the users gets exposed, and their state leaks to the adversary. Then all subsequent messages sent using the Double Ratchet protocol will become susceptible to HNDL attacks again, as new secrets are still exchanged using elliptic-curve cryptography.
A fully post-quantum Double Ratchet protocol for Signal
In a recent collaboration with Signal’s Rolfe Schmidt, and Yevgeniy Dodis and Daniel Jost at NYU, we (i.e., PQShield’s Benedikt Auerbach, Shuichi Katsumata, and Thomas Prest) investigated how to upgrade Signal’s Double Ratchet protocol to achieve full post-quantum security. In two research papers, published at Eurocrypt 2025 and USENIX Security 2025, we developed and compared several protocols, one of which serves as a basis of the new Triple Ratchet protocol that has now been released by Signal on October 2nd, 2025. Cryspen then partnered with Signal to formally analyse the security of the protocol design and ensure that the deployed code of the Triple Ratchet protocol is implemented correctly and securely.
At a high level, the idea behind the Triple Ratchet protocol is to extend the Double Ratchet by incorporating an additional, post-quantum secure, public-key ratchet named Sparse Post-Quantum Ratchet (SPQR). (To be precise, SPQR is the combination of a novel public-key ratchet denoted ML-KEM Braid and a symmetric ratchet. To keep things simple, however, we will not distinguish between the two in this blog.) The keys used to encrypt application messages are derived from the shared secrets established by both classical and post-quantum public-key ratchets.
The solution is tailored to Signal’s specific requirements by
- providing hybrid security, while
- only introducing a small overhead in terms of protocol message size.
The former essentially means that if one considers attacks with a classical computer, it would be necessary to break both the elliptic-curve based cryptography and the post-quantum key exchange in order to successfully attack the protocol. For the post-quantum scheme, ML-KEM was selected, the same KEM already used by PQXDH. Aiming for hybrid security can be seen as conservative design, as it benefits from widely deployed elliptic-curve cryptography as a fallback system instead of relying solely on the more novel post-quantum solution.
The main technical challenge we had to overcome in our work, and the focus of the more detailed discussion below, is the second point. Concretely, Signal aimed for a scheme where the “post-quantum” protocol messages were comparable in size to the Double Ratchet protocol messages — around 36 bytes. However, in the context of post-quantum cryptography this restriction is dauntingly small: For example, the ML-KEM parameter set used, ML-KEM-768, has public keys consisting of 1184 bytes and ciphertext of 1088 bytes, an order of magnitude larger than classical counterparts. Looking ahead, this is why the additional public-key ratchet sends its protocol messages in small chunks that, after a sufficient number have been received, are recombined into ML-KEM public keys and ciphertexts. While this idea is quite simple, it turned out to open up quite a large protocol design-space and enabled several subtle optimizations that help us to improve the protocol’s FS and PCS guarantees. We will dive into the details below.
The Triple Ratchet Protocol
At a high level, the Triple Ratchet Protocol combines symmetric ratcheting with two public-key ratchets, one of which is required to be post-quantum secure. (To be precise, each public-key ratchet uses a separate symmetric ratchet, the outputs of which are in turn combined using a key-derivation function to generate the keys used to encrypt application messages.) In the following we go into the details of the post-quantum ratchet. To establish some notation, we refer to the encrypted text messages as application messages and to the ones generated by the public-key ratchet and sent along with them as protocol messages.
A naive post-quantum-secure public-key ratchet
To get a better understanding of public-key ratchets we can consider a simple protocol template by Alwen, Coretti, and Dodis (Eurocrypt 2019) that makes use of key-encapsulation mechanisms (KEM). KEMs are a cryptographic primitive that allows users to generate key pairs consisting of a public key pk and a secret key sk. Given the public key, one can generate ciphertext ct which encapsulates a secret K as (K,c) = Enc(pk). While K remains hidden from outsiders, it can be recovered using the secret key as K = Dec(sk,c). In our application of KEMs, K will take the role of the shared secrets infused in the symmetric ratchet.
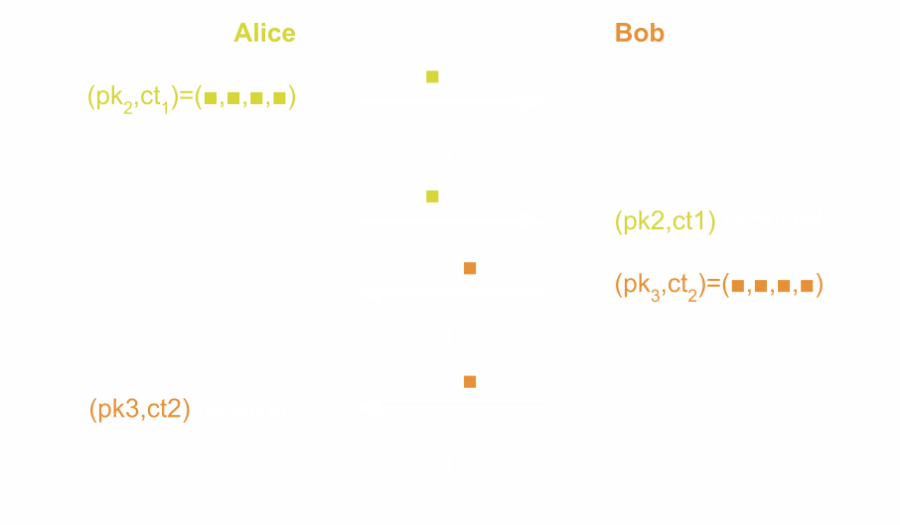
Equipped with a KEM, we can construct a public-key ratchet as depicted below. The two parties denoted Alice and Bob exchange protocol messages to generate a sequence of shared secrets. Looking ahead, these secrets are infused in the symmetric ratchet in the Triple Ratchet protocol to enable PCS. Assume that user Alice already possesses a public key pk1 generated by Bob. Alice simply encapsulates a secret
(K1, ct1) = Enc(pk1)
under public key pk1 and sends the corresponding ciphertext to Bob. However, since Bob needs to be able to encapsulate secrets to Alice as well, Alice also generates a key pair (pk2, sk2) and includes pk2 in the protocol message sent to Bob. After receiving the message, Bob has Alice‘s updated public key and is able to recover K1 from the ciphertext. Since every public key is supposed to be used only once, Bob deletes sk1 afterwards. Now the users’ roles reverse, with Bob taking on the role of the sender.
To get an intuition of why the construction achieves PCS, let’s assume, for example, that Bob was briefly compromised and their internal state including sk1 leaked to an adversary. In this case, the first protocol message sent by Alice is insecure as the adversary is able to recover K1 by simply decrypting the corresponding ciphertext. Afterwards, however, Bob will encapsulate the next secret K2 under the freshly generated public key pk2. As a consequence K2 cannot be decrypted by the adversary. Further, Bob replaces their compromised key sk1, so future messages from Alice will also no longer leak the encapsulated secret, and we achieve PCS.
With this simple protocol in place, it seems we are already done with the task of creating a post-quantum secure public-key ratchet. And indeed, by simply plugging ML-KEM in the construction, we obtain a protocol meeting our security goals.
Challenges and our solution
Inspecting our candidate solution closer, we run into an immediate issue. ML-KEM’s public keys and ciphertexts are far too large for Signal’s requirements: Recall that a protocol message needs to transmit both a public key and a ciphertext, which results in a protocol message of
2272 B = 1184 B + 1088 B.
A median Signal message, on the other hand, currently is of size 66B, which includes both the Double Ratchet message and the payload. So, using the simple solution outlined above would lead to an unacceptable size increase by a factor of ~35x!
SPQR overcomes this challenge by carefully combining two ideas.
We first make use of chunking, i.e., breaking the large protocol messages into small chunks using erasure codes (as explained below), and transmitting one chunk with every application message. However, since breaking up the post-quantum message means more messages have to be sent in order to establish a (post-quantum-secure) shared secret, the post-quantum ratchet achieves PCS at a much slower rate. We therefore amend this issue by an optimization technique we call opportunistic sending. We detail both of these ideas below.
Chunking
To break protocol messages into small chunks, SPQR makes use of erasure codes, a well-known tool from coding theory. Given a protocol message m=(pk, ct) such a code allows Alice to continuously generate a stream of small chunks ch1, ch2, ch3, … of a preset size that then can be sent to the other party. Bob, after receiving a sufficient amount of chunks, is able to recover m and from it the new shared secret. Now Bob takes over the role of sender, generates a (large) protocol message, and starts sending chunks of it.
A feature of Signal’s Double Ratchet is that it achieves immediate decryption. This is the requirement that application messages can be decrypted even if they arrive out of order or, even worse, some messages get dropped. Erasure codes lend themselves naturally to preserving this feature: For the reconstruction of message m it is not necessary that all chunks were transmitted successfully, but only that Bob received any collection of them, as long as it is sufficiently large.
Regarding the security of our chunked protocol, note that, as opposed to the simple protocol discussed above, a new shared secret is no longer generated with every protocol message. Instead, many messages have to be transmitted in order for Bob to receive K. This is why it is called a Sparse PQ Ratchet. As a consequence, SPQR achieves post-quantum PCS at a slower rate.
Opportunistic Sending
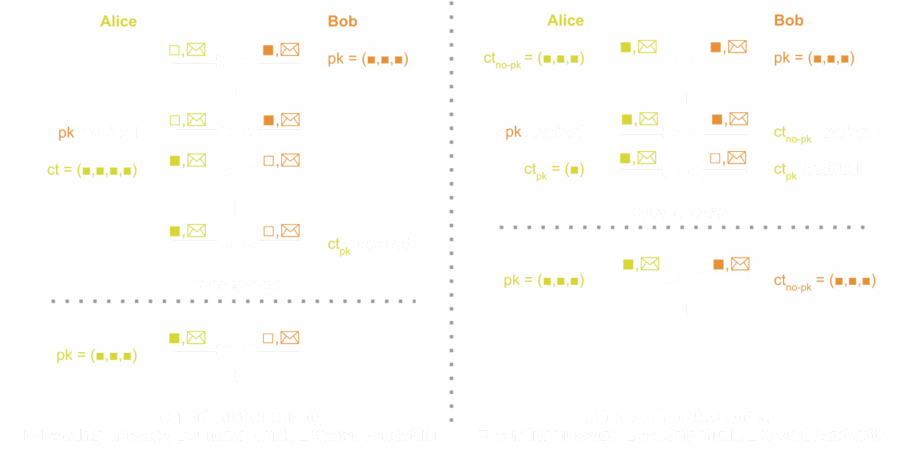
In the chunking protocol as described above, the party currently receiving chunks is not able to transmit any cryptographic material. Instead, they have to wait their turn to take over the role of the sender. If we consider application messages, however, we would expect both parties to communicate at a similar rate, with texts being sent in both directions (See the figure below, left side). Since only about every second application message is accompanied by a chunk of a protocol message, a lot of bandwidth is wasted that could be used to send cryptographic material and in turn speed up PCS.
In our research we observed that for typical public-key ratchet constructions some of the cryptographic material that is sent as part of a protocol message is independent of the other party’s current or prior protocol message. Thus, the party, say Bob, could also sample this part of the message early and already start sending chunks concurrently to the other party. As a consequence, when it is ‘Bob’s turn to send’ they will be able to send the remaining part of the message in fewer messages, intuitively speeding up the rate at which PCS is achieved. We call this idea opportunistic sending.
Concretely, we observe that for a typical lattice-based KEMs, including ML-KEM, the ciphertext consists of two components
ct = (ctno-pk,ctpk) = (D ⋅ r + z, pkTr + z’ + ⌊q/2⌉ ⋅ K).
Here, D and q are public parameters of the scheme and r and z are vectors sampled during the generation of the ciphertext. Note that a ciphertext’s first part ctno-pk is independent of the public key. Furthermore, ctno-pk is typically substantially larger than ctpk — for ML-KEM-768, ctno-pk is 960 bytes while ctpk is only 128 bytes. As a consequence, in the chunking protocol described above the ‘sending’ party can start sending parts of the ciphertext, i.e., the large ctno-pks, while still receiving chunks of the corresponding public key (See Figure 5, right), where ctno-pk and pk have roughly the same size for ML-KEM. Thus, assuming the communication is balanced, Alice and Bob no longer ‘waste’ their bandwidth since they don’t have to idly wait before sending their chunks. Since ctpk is small, only a few application messages are wasted by not having an accompanying chunk, and therefore, we achieve PCS at a faster rate, lowering the negative impact chunking has on post-quantum PCS.
Putting everything together
By combining the ideas described above, we essentially end up with Signal’s new Triple Ratchet protocol. To briefly recall, its components are
- the new post-quantum-secure Sparse Post-Quantum Ratchet (SPQR).
- the elliptic-curve based classically secure DH ratchet, and
- the symmetric ratchets.
SPQR essentially implements the chunking and opportunistic sending solutions described above with ML-KEM using 42-byte chunks. However, due to some of the inner workings of ML-KEM, it slightly differs from the simplified description of the previous paragraph. Concretely, in ML-KEM ctno-pk cannot be generated completely independently of the corresponding public key. Accordingly, in SPQR the sending party has to wait until they receive a short ‘header’ derived from pk, before they can generate ctno-pk and send it concurrently to receiving pk.
Due to the use of chunking in SPQR, the two public-key ratchets do generate shared secrets at different rates. This makes the inclusion of said shared secrets into the symmetric ratchet a bit more involved. We refer to the Eurocrypt 2025 and USENIX Security 2025 publications for additional details on how this is handled.
As briefly discussed above, due to the use of two public-key ratchets, the protocol is hybrid secure. This means an adversary has to break both of the public-key ratchets in order to recover all shared secrets and decrypt application messages. Thus, we not only gain benefits in terms of post-quantum security, but with respect to classical adversaries the scheme’s security guarantees are at least as good as before: The DH ratchet infuses the same amount of shared secrets into the symmetric ratchet as was the case for the Double Ratchet, while SPQR only adds to this.
Outlook: potential future optimizations
As part of our research into post-quantum secure public-key ratchets, we also considered an optimization orthogonal to opportunistic sending: Recall that for ML-KEM-like KEMs the ciphertexts take the form
ct = (ctno-pk,ctpk) = (D ⋅ r + z, pkTr + z’ + ⌊q/2⌉ ⋅ K).
Futher, public keys are defined as
pk = D ⋅ s + e,
where again D is a public parameter and s and e are vectors sampled according to a particular distribution. We can observe that pk essentially has the same structure as ctno-pk, the first part of a ciphertext. Since in our public-key ratchet protocol users have to transmit both a ciphertext and a public key, this observation leads to whether it is possible to simply reuse ctno-pk as the next round’s public key. This would essentially cut the communication cost of a protocol message in half. In fact, Signal’s Diffie-Hellman ratchet makes a similar optimization. Here, every round a single element of an elliptic curve, that we can interpret as both a ciphertext and a public key, is sent as the protocol message. In the Eurocrypt 2025 paper, we were able to show that this idea can indeed be adapted to lattice-based KEMs, albeit at the cost of having to increase the parameter size of the underlying lattice. Nevertheless, the resulting ratcheting KEM, called Katana, is able to save about 40% in terms of combined public key and ciphertext size over ML-KEM-768. Thus, plugged into the public-key ratchet template described above, it achieves PCS at a faster rate.
In the USENIX Security 2025 paper, we compare an optimized version of the resulting public-key ratchet that additionally makes use of opportunistic sending to several other constructions. Overall, it performs similar to SPQR, but seems to have a slight edge as its PCS guarantees with respect to the two users are more symmetric. So, it could be an attractive candidate to potentially replace SPQR at some point. However, since its lattice parameters differ from the NIST-standardized ML-KEM and the scheme has not yet been formally verified, more confidence in the construction is necessary before being considered for deployment in practice.
This blog was authored by Dr. Benedikt Auerbach, Dr. Shuichi Katsumata, and Dr. Thom Wiggers. Find more PQShield research in our Publications Archive.

