Behind every transaction, every secure message and every point of access to secure systems, cryptography is working to help ensure confidentiality, integrity, and authenticity. It’s the mathematical foundation of our digital security. But what if this foundation has a crack? That’s where formal verification comes in – a technology that uses deep mathematical proofs and logic to guarantee a system’s security, and it’s an area that our Research Team specialize in. In this, the first of a series of technical blogs, our world-class researchers take you through the centrality and importance of Formal Verification as a safeguard, especially for the cryptographic algorithms that are being deployed for post-quantum transition…
Introduction
Formal verification is a technology that permits relying on machines to validate the properties of software and hardware systems. Formal verification tools rely on solid mathematical foundations and therefore permit significantly increasing the level of assurance provided by an implementation. For this reason they are usually associated with security-critical systems and critical infrastructure in general.
Cryptographic algorithms are a foundational part of the IT infrastructure that is critical to our society. They underpin the confidentiality, integrity, and authenticity of digital information. Any flaw in their implementation can lead to catastrophic security breaches. For this reason, formal verification is being increasingly used in the development of high-assurance cryptography implementations.
The rigorous approach provided by formal verification is particularly crucial for the new and complex algorithms that are being rolled out for the post-quantum transition. This process will have a huge impact on the existing IT infrastructure, and formal verification will play an important role in guaranteeing that, in addition to mitigating the risks that may come from a potential breakthrough in quantum computing, the modifications to the IT infrastructure do not introduce new vulnerabilities against known and unforeseen threats, thereby ensuring the long-term security and trustworthiness of cryptographic systems.
Formal verification in cryptography
Formal verification, in the context of cryptographic implementations, involves multiple critical aspects that together ensure the security and correctness of cryptographic systems.
- Definition of a secure cryptographic primitive
- Alignment with the formal specification
- Resistance to low-level attack
The first aspect focuses on verifying that the specification itself defines a secure cryptographic primitive. This involves proving that the specified algorithm meets its intended security goals, such as ensuring confidentiality, integrity, and authenticity, against a range of adversarial attacks. By formalizing security notions and proving that the algorithm satisfies these notions under certain hardness assumptions, developers can ensure that the cryptographic primitive is theoretically robust and resistant to attacks.
The second aspect is verification that the implementation of a cryptographic primitive faithfully follows its formal specification, i.e., that it is functionally correct. This process involves creating a precise mathematical model of the specification and then, using formal methods, such as model-checking or theorem-proving, ensuring that the implementation adheres strictly to this model under all possible conditions. It’s an essential step because even if the specification is correct, any deviation in the implementation can introduce vulnerabilities that compromise security.
A stepping stone to functional correctness—typically requiring a fraction of the resources and expertise—formal verification also covers the goal of ensuring program safety, particularly concerning memory safety and the avoidance of undefined behaviour. This involves proving that the implementation is free from common programming errors such as buffer overflows, null pointer dereferences, and other forms of undefined behaviour that could be exploited to undermine the security of the cryptographic primitive. Ensuring memory safety and preventing undefined behaviour are essential for maintaining the integrity of the cryptographic system, as these types of errors can lead to unpredictable behaviour, potentially exposing the system to severe vulnerabilities.
The third aspect of formal verification addresses the implementation’s resistance to low-level attacks, such as side-channel attacks or fault attacks, which exploit physical or timing-related properties of the system. In this case, formal methods are used to model potential side channels and prove that the implementation does not inadvertently leak sensitive information through these channels, ensuring that the system’s behaviour is independent of secret data with respect to timing, power consumption, or other measurable parameters.
By integrating these three aspects – secure specification, correct implementation and resistance to low-level attacks, formal verification provides a comprehensive approach to building trust on the robustness of cryptography implementations and their ability to deliver the intended level of security in real-world applications.
How formal verification compares to testing (CAVP / TVLA)
Formal verification and testing methods, such as CAVP (Cryptographic Algorithm Validation Program) for functional correctness and TVLA (Test Vector Leakage Assessment) for leakage assessment, serve as complementary approaches in ensuring the security and reliability of cryptographic implementations. However, these methods differ significantly in their methodologies, scope, and the level of assurance they provide.
Testing methods like CAVP and TVLA rely on empirical approaches to validate cryptographic implementations.
CAVP approaches functional correctness by running a series of predefined tests to ensure that the implementation produces correct outputs for specific inputs, ensuring compliance with established standards and confirming the implementation’s correct behaviour in practical scenarios. However, this approach is inherently limited because it typically only tests the implementation against a small part of the inputs that may occur in practical scenarios. This means that errors or vulnerabilities in untested cases may go undetected.
TVLA assesses an implementation’s resistance to side-channel attacks by analysing, over physical observations, whether its behaviour correlates with secret data. It is effective in identifying potential side-channel vulnerabilities through statistical analysis of test vectors. Yet, like CAVP, it is limited by the scope of the tests and the quality of the statistical analysis; it cannot provide absolute guarantees that the implementation is free from side-channel leakage in all possible operating conditions.
Formal verification involves using mathematical proofs to verify that a cryptographic implementation strictly adheres to its formal specification and that the specification itself meets the required security properties. This approach guarantees that the implementation behaves correctly under all possible inputs and conditions, offering a more comprehensive assurance of correctness. Because it involves proving properties across all possible scenarios, formal correctness permits identifying and eliminating subtle bugs or security flaws that might otherwise go undetected.
However, formal verification is resource-intensive, requiring specialised expertise, significant time, and considerable computational resources. It can also be challenging to apply to very large or complex systems, and its effectiveness hinges on the accuracy and completeness of the formal model and specifications. Indeed, the Trusted Code Base of formal verification tools can, itself, be quite large. Moreover, formal verification always works over a model of reality, which may not be sufficiently accurate to capture all real-world attacks. Formal verification should therefore not be seen as a substitute for other validation methods, but rather a way to complement them and upgrade the level of assurance.
In short, testing methods like CAVP and TVLA, while more practical and accessible, provide assurance within a limited scope and cannot guarantee the absence of all possible issues. Nevertheless, they are invaluable for validation – particularly for confirming functional correctness, and detecting specific vulnerabilities in real-world scenarios – because they permit detecting problems that may be out of scope of formal verification results.
In comparison, formal verification offers a higher level of assurance due to its reliance on mathematical proofs, which can definitively demonstrate the absence of certain types of errors or vulnerabilities if correctly applied. However, this comes at a cost: formal verification may require significantly more resources and specialised knowledge.
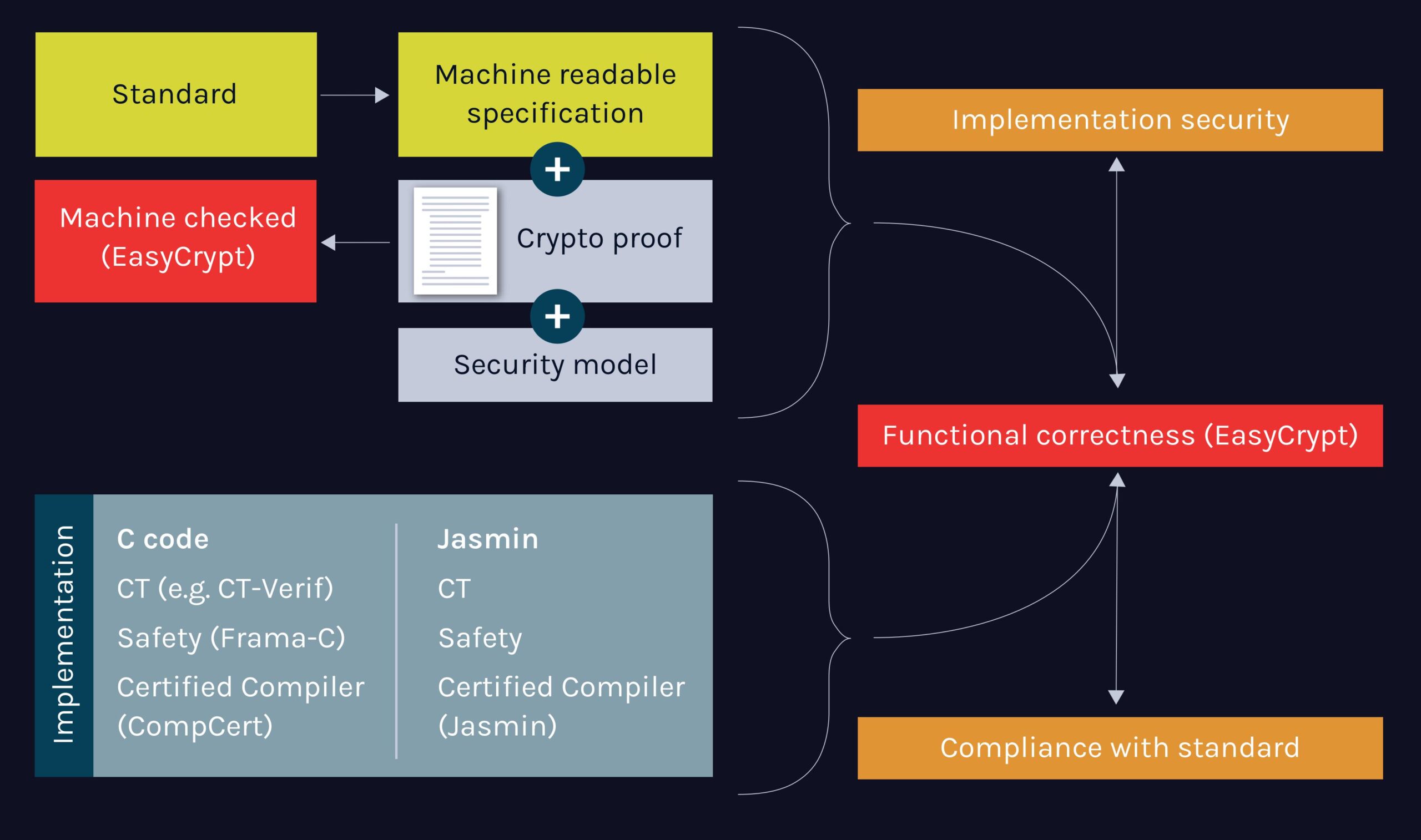
The challenge is therefore to find the correct combination of formal verification and testing methods to ensure that an implementation meets the level of assurance required by specific target applications, at justifiable cost.
PQShield’s Current Offerings and Roadmap
At PQShield, we have invested in formal verification to reinforce the security of our algorithms and protocols. As a participant in the Formosa-Crypto project, which brings together various initiatives focused on machine-checked cryptography and high-assurance cryptographic engineering, we are committed to several key research efforts that we will present in a sequence of upcoming blog posts on the topic.
A core component in this effort is the development of the open-source verification tool, EasyCrypt – a proof assistant for reasoning about cryptographic algorithms at various levels of abstraction, ranging from abstract security proofs to low-level implementations. PQShield is currently the lead developer of the tool, which serves as the trusted backend for all the formal verification work carried out by the Formosa-Crypto project in formally verifying designs and implementations of the recently approved and upcoming Post-Quantum Cryptography standards.
Our researchers are actively contributing to projects such as the verification of cryptographic security for the most relevant FIPS standards, including ML-KEM, ML-DSA, SLH-DSA and SHA-3 itself, and also the hash-based signature standard XMSS. Additionally, we are working on a comprehensive end-to-end verification process, covering security, functional correctness, and constant-time verification of implementations of these standards. This process is complete for optimized implementations of ML-KEM for the x86-AVX2 architecture, and others are work in progress undertaken by a growing international team.
This expertise is directly applied to our internal projects. We have already begun efforts to prove the safety and correctness of PQCryptoLib, our portable software library that implements the new NIST post-quantum cryptography standards. For example, we proved our implementations of the SHA-3 block permutation (Keccak), including the high-speed vectorized implementations for both AVX2 and ARM Neon. We have also finalized the safety proof and the full functional correctness of the low-level components of our PQCryptoLib ML-KEM implementation: polynomial arithmetic (including the AVX2 NTT), decoding/encoding functions, rejection sampling. In 2026, we will further advance this work on our general-purpose ML-DSA implementation, along with customer-specific versions of ML-DSA/ML-KEM.
This verification process uses a mixture of open-source verification tools (some of which we co-develop) and internally-developed verification tools.
Conclusion
The emergence of new post-quantum cryptography standards and their upcoming adoption implies that the IT infrastructure will suffer a rapid transformation in the next few years. New implementations and designs will be deployed in a very short time, which increases the risk of new vulnerabilities being introduced as a byproduct of the post-quantum migration.
Formal verification is a valuable technology for eliminating vulnerabilities from cryptographic systems before they are deployed. It increases assurance by rigorously proving that implementations satisfy safety, correctness and security properties for all possible inputs. While resource-intensive and reliant on precise specifications, it complements traditional testing methods like CAVP and TVLA.
PQShield is not only integrating formal verification into its cryptographic offerings but also actively advancing the state of the art. Through contributions to tools like EasyCrypt, and participation in innovative projects, PQShield continues to demonstrate its commitment to driving the field forward, delivering cutting-edge, secure, and reliable cryptographic solutions. In a series of upcoming blog posts we will provide more details on these projects.

